Об одной особенности принятия решения врачом

А.П. Хускивадзе

Аннотация

В статье рассматриваются задачи принятия решения врачом при малых и репрезентативных выборках результатов обследования больного. Изыскивается общий способ решения этих задач.

Статья представляет интерес как для врачей-практиков, так для медиков-исследователей, а также и для специалистов, работающих в областях прогнозирования и принятия решения.

Все права на материалы статьи защищены, и эти материалы не могут быть использованы без письменного разрешения владельца авторских прав и Федеральной службы по интеллектуальной собственности, патентам и товарным знакам РФ.

Ключевые слова: принятие решения, прогнозирование, врач-практик, малая выборка, репрезентативная выборка.

Постановка задачи

В настоящее время при лечении конкретного больного, как правило, оперируют фактическими данными

B_j1 = {b_jλ¹ ; λ = 1..N_j1; 1≤ N_j1 ≤ 5 }; j = 1..N , (1)

где

b_jλ¹ - – количество замеров величины y_j Î Y;

Y – генеральная совокупность первичных показателей состояния больного.

И в подавляющем большинстве случаях состояние больных улучшаются. Следовательно, эти данные содержат информацию, достаточную для принятия правильного решения с вероятностью, близкой 1.

Возникает вопрос: можно ли извлекать эту информацию? И, если да, то как?

Чтобы ответить на эти вопросы, в первую очередь, следует выяснить, чем различие между задачей, стоящей перед врачом – практиком и задачей, стоящей перед медиком – ученым?

Задача прогнозирования состояния здоровья человека

При решении задачи прогнозирования состояния типичного представителя (ТП) однородной группы больных с целью получения обобщенных научных выводов, необходимо знание совокупностей данных

B_j1(G); j = 1..N (2)

и

B_j0(G); j = 1..N (3),

где совокупность данных (2) служит объективной характеристикой изучаемого состояния ТП, а совокупность (3) является объективной характеристикой возможного нормального состояния ТП.

На практике вместо совокупностей (2) и (3), оперируют данными

B_j1 = {b_jλ¹ ; λ = 1..N_j1}; j = 1..N

и (4)

B_j0 = {b_jλ⁰ ; λ = 1..N_j9}; j = 1..N,

где

B_j1 - совокупность фактических результатов обследования части больных, служащая репрезентативной выборкой от B_j1(G)с доверительной вероятностью

P = P₀ ≥ 0.95; (5)

B_j0 - совокупность фактических результатов обследования части здоровых людей, служащая репрезентативной выборкой от B_j0(G) с доверительной вероятностью P = P₀ ≥ 0.95.

В далее мы будем полагать, что выполняются следующие два условия [2 ]

Условие 1

Каждая выборка

B = B_{j 0} + B_{j 1}

представляет собой результаты равноточных и взаимно независимых измерений величины

y_j Î Y.

Условие 2

Систематические ошибки измерения величины y_j Î Y отсутствуют, а случайные ошибки ее измерения описываются нормальным законом распределения вероятностей

Обозначим

и S_{j 1} = ; j = 1..N

и (6)

d_jk = S_jk 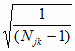и t_jk= t_j(P, (N_jk – 1)); k = 0,1,

где

t_jk - критическое значение критерия Стьюдента при степени свободы (N_jk – 1).

Из репрезентативности выборок (4) следует, что

ç Μ_{j k} - Μ_{j k}(G) ç < d_{j k} t_{j k}; k = 0,1, (7)

где

Μ_{j k}(G) – генеральное среднее арифметическое величины Μ_{j k}.

Зависимость (7) имеет смысл в том случае, когда

d_{j k} t_{j k} > 0; k = 0,1

Отсюда и из (5) и (6) следует, что

1<< N_{j k} < ∞; k = 0,1 (8)

Таким образом, решая задача прогнозирования, всегда должны оперировать выборками данных, для которых выполняются условия (7) и (8).

Проблема учета особенностей организма индивида

Пусть, Δ_j(П) – абсолютная погрешность измерительного прибора величины y_j Î Y,

где

Y – генеральная совокупность первичных показателей состояния больного.

По мере усовершенствования техники измерения величина Δ_j(П) становится все меньше и меньше. Тем не менее, можно полагать, что

Δ_j(П) > 0

Ясно, что величина y_j Î Y наиболее точно может быть измерена в единицах Δ_j(П).

Вообще

│Δ_j(O) - Δ_j(П)│≥ 0; j = 1..N, (9)

где

Δ_j(O) – единица измерения величины y_j Î Y, фактически используемая при определении состояния здоровья данного больного.

Пусть

M_j1(O) и S_{j 1}(O); j = j₀; j₀= 1..N

- значения

M_j1 и S_{j 1}; j = j₀; j₀= 1..N ,

установленные в результате измерения величины y_j Î Y в единицах Δ_j(O):

M_j1(O) = M_j1 и S_j1(O) = S_j1 при Δ_j(O) = Δ_j(П) ; j = 1..N (10)

Пусть

M_j1(O,G) и S_{j 1}(O,G); j = 1..N (11)

являются значениями

M_j1(O) и S_{j 1}(O); j = 1..N

такими, что имеют место

M_j1(O) = M_j1(O,G) и S_j1(O) = S_j1(O,G) при Δ_j(O) = 0 ; j = 1..N (12)

В чем сходство и различие между величинами M_j1(O,G) и M_j1(G)?

Величина M_j1(G), как генеральная среднее арифметическая, является объективной характеристикой фактического состояния типичного больного (ТП) изучаемой однородной группы больных, Для этой величины всегда имеет место: Δ_j(G) = 0,

где

Δ_j(G) – абсолютная ошибка измерения M_j1(G).

Для величины M_j1(O,G), в отличие от M_j1(G), на практике, как правило, имеет место

Δ_j(O) > 0; j = 1..N (13)

Поэтому, вместо (12), в общем случае должно выполняться условие

M_j1(O) Î A_j(О,G); j = 1..N , (14)

где

A_j(O,G) = (M_j1(O,G) - Δ_j(O) , M_j1(O,G) + Δ_j(O)); j = 1..N (15)

Если условие (14) выполняется, то можно сказать, что у больного измерение величины y_j Î Y произведено корректно. В противном случае, измерение будет выполнено некорректно.

Из (14) и (15) имеем

M_j1(O,G)Î A_j(O) ; j = 1..N , (16)

где

A_j(O) = (M_j1(O) - Δ_j(O) , M_j1(O) + Δ_j(O)); j = 1..N (17)

Таким образом, если мы будем знать

M_j1(O) и Δ_j(O) ,

то с точностью Δ_j(O) ≥ 0 можно установить и величину M_j1(O,G).

Итак, величина M_j1(G) всегда измеряется с точностью Δ_j(G) = 0, а величина M_j1(О,G) измеряется с точностью Δ_j(O) ≥ 0.

При этом, если данный больной является ТП изучаемой однородной группы больных, то имеет место

M_j1(O,G) = M_j1(G) при Δ_j(O) = Δ_j(G) = 0

и (18)

Δ_j(O) >│M_j1(O,G) - M_j1(G)│> 0 при Δ_j(O) > 0

Во всех других случаях имеет место

Δ_j(Н,G) >│M_j1(O,G) - M_j1(G)│≥ Δ_j(O) > 0, (19)

где

Δ_j(Н,G) – значение величины y_j Î Y такое, что имеет место

A_j(Н,G) = (M_j1(G) - Δ_j(Н,G) , M_j1(G) + Δ_j(Н,G)); j = 1..N

Об области A_j(Н,G) говорят, что она является областью неразличимости значений величины

y_j Î Y для изучаемой однородной группы больных.

О величине Δ_j(Н,G) можно говорить, что она является единицей измерения величины

y_j Î Y для изучаемой однородной группы больных.

Возникает вопрос: какую из величин M_j1(O,G) и M_j1(G) следует отдать предпочтение?

В природе двух неразличимых друг от друга людей не бывают. Даже братья-близнецы в чем-то друг от друга различаются. Поэтому и говорят: каждый человек имеет свою неповторимую индивидуальность.

Различие индивидуальностей друг от друга обусловлено многими и многими факторами.

Обозначим всю совокупность факторов, способствовавших формированию личности данного больного через L(O).

Положим, что существует человек, представляющий собой ТП изучаемой однородной группы больных. Совокупность факторов, способствовавшая формирование личности этого человека, обозначим через L(ТП).

Если данный больной является ТП изучаемой однородной группы больных, то L(O). = L(ТП) и, следовательно, имеет место (18). Во всех других случаях L(O). ¹ L(ТП) и, следовательно, выполняется условие (19).

Величина M_j1(O,G) получена вследствие существования данного больного в среде L(O). Следовательно, мы поступим правильно, если при лечении этого больного отдадим предпочтение величине M_j1(O,G). В этом случае мы допустим меньшую ошибку при принятия решения.

Величина M_j1(G) получена вследствие существования типичного больного в среде L(ТП). Следовательно, мы поступим правильно, если при решении задачи прогнозирования отдадим предпочтение величине M_j1(G).

Итак, при лечении конкретного больного следует взять в качестве ориентира величину M_j1(O,G), а при решении задачи прогнозирования в качестве ориентира следует взять величину M_j1(G).

Пусть

M_j(Z); S_j (Z); M_j(Z,G) и S_j (Z,G); j = 1..N

являются значениями

M_j1(O); S_{j 1}(O,G); M_j1(O,G) и S_{j 1}(O,G); j = 1..N

такими, что если человек находится в нормальном состоянии, то

M_j1(O) = M_j(Z); S_j1(O) = S_j1(Z,); M_j1(O,G) = M_j(Z,G) и S_j1(O) = S_j1(Z, ,G)

при Δ_j(O) = 0; j = 1..N

О величине M_j(Z,G) говорят, что она является объективной точечной индивидуальной нормой человека, а M_j(Z) является оценкой M_j(Z,G).

Согласно (12) величина M_j(Z,G) является одним из возможных значением M_j1(O,G). Следовательно, величиной M_j1(O,G), как и величиной M_j(Z,G), человек характеризуется как индивидуальность. В этом и состоит преимущество ориентирования при лечении конкретного больного на величину M_j1(O,G), а не на величину M_j(G).

Для определения величины M_j1(O,G), согласно (16) и (17), необходимо и достаточно, чтобы выполнялось условие

ç Μ_{j 1}(O) - Μ_{j 1}(O,G) ç < Δ_j(O); j = 1..N (20)

Если это условие выполняется, то можно написать, что: Μ_{j 1}(O,G) » Μ_{j 1}(O) .

Как видно, при лечении конкретного больного достаточно знание данных

M_j1(O) и Δ_j(O); j = 1..N

и совершенно не требуется знание данных

Μ_{j 1}(G); j = 1..N

Следовательно, нет необходимости выполнения условия

ç Μ_{j 1} - Μ_{j 1}(G) ç < d_{j 1} t_{j 1}; j = 1..N (21)

Однако остается необходимость выполнения условия

ç Μ_{j 0} - Μ_{j 0}(G) ç < d_{j 0} t_{j 0}; j = 1..N (22)

Дело в том, что величины

Μ_{j 0}(G) ; j = 1..N

служат объективными характеристиками возможного нормального состояния данного больного.

Следовательно, для их установления, как ожидаемых - прогнозируемых - величин, необходимо решение задачи прогнозирования. Но условие (22), как было показано выше, может выполняться только в том случае, когда

N_{j 0} >> 1; j = 1..N

Точнее, должно иметь место

N_{j 0} ≥ N_{j min}; j = 1..N ,

где

N_{j min} - значение N_{j 0} при котором выборка B_j0 является репрезентативной с доверительной вероятностью P = P₀ ≥ 0.

В отличие от (22), условие (16), согласно (17), может выполняться как в том случае, когда

N_{j 1} = 1; j = 1..N ,

так и в том случае, когда

N_{j 1} > 1; j = 1..N .

Здесь важно лишь то, что величина M_j1(O) была получена по результатам измерения величины

y_j Î Y с точностью Δ_j(O ).

В итоге, при лечении конкретного больного можно оперировать совокупностями данных, для которых имеют место

N_{j 1} ≥ 1 и N_{j 0} >>1; j = 1..N

Особенности принятия решения по единичным результатам обследования

состояния здоровья человека

В настоящее время при лечении конкретного больного, как правило, оперируют фактическими данными (1). И в подавляющем большинстве случаях состояние больных улучшаются. Следовательно, эти данные, как указывалось выше, содержать информацию, достаточную для принятия правильного решения с вероятностью, близкой 1.

Как это информация из совокупности (1) извлекается?

Вообще величины

y_j Î Y и y_i Î Y; j,i = 1..N ; j ¹ i (23)

имеют различные размерности и, следовательно, как сами они, так их общепринятые единицы измерения

Δ_j(П) и Δ_i(П) ; j,i = 1..N ; j ¹ i , (24)

являются между собой несопоставимыми.

Следовательно, величины

Μ_{j k} и Μ_{i k}; k = 0,1; j,i = 1..N ; j ¹ i , (25)

тоже являются между собой несопоставимыми.

Врач, оперируя фактическими данными, для которых имеет место (1), как указывалось выше, подавляющее большинство случаев, принимает обоснованное решение. Это ему удается сделать благодаря тому, что данные фактического состояния больного (25) он каким-то образом все же сопоставляет как между собой, так и с данными возможного нормального состояния этого больного. Именно этим путем врачу и удается компенсировать недостающие, с точки зрения математической статистики, данные.

Пусть, имеет место

ç Μ_{j 0} - Μ_{j 0}(G) ç < Δ_{j 0} , (26)

где

Δ_{j 0} = dj ₀ t_{j 0} (27)

Тогда с доверительной вероятностью P = P₀ утверждают, что

Μ_{j 0} = Μ_{j 0}(G)

Тем самым, по сути дела, все значения величины y_j Î Y, принадлежащие открытой области

(Μ_{j 0}(G) - Δ_{j 0} , Μ_{j 0}(G) + Δ_{j 0} ),

рассматривают, как практически друг от друга неразличимые. Вместе с тем в закрытой области

A_j0(G) = [Μ_{j 0}(G) - Δ_{j 0} , Μ_{j 0}(G) + Δ_{j 0} ]

друг от друга различают три значения величины y_j Î Y. Ими являются значения

y_j = Μ_{j 0}(G) - Δ_{j 0}, y_j = Μ_{j 0}(G) и y_j = Μ_{j 0}(G) + Δ_{j 0}

Таким образом, при заданной доверительной вероятности P = P₀ в области A_j0(G) величина y_j Î Y фактически измеряют не с точностью Δ_j (П), а с точностью Δ_{j 0}. В итоге, в области A_j0(G) величина y_j Î Y наиболее точно можно измерить в единицах Δ_{j 0} ≥ Δ_j (П).

Вообще имеет место

A_j0(G) ÍÍ A_j,

где

A_j – область задания величины y_j Î Y.

Если выполняется условие (26) и, следовательно, y_jÎ A_j0(G), то, согласно (7), величина y_j Î Y находится в пределах области общепринятой статистической нормы. А если условие (26) не выполняется, то имеет место

y_{j Î} (A_j - A_j0(G))

В этом случае говорят, что величина y_j Î Y находится вне области общепринятой статистической нормы.

В том случае, когда величина y_j Î Y находится вне области общепринятой статистической нормы, возникает необходимость проверки условия

çΜ_j1 - Μ_j1(G) ç < Δ_j1 , (28)

где

Δ_j1 = dj₁ t_j1 (29)

Если условие (28) выполняется, то с доверительной вероятностью P = P₀ можно утверждать, что

Μ_j1 = Μ_j1(G)

Обозначим

A_j1(G) = [Μ_j1(G) - Δ_j1 , Μ_j1(G) + Δ_j1 ]

В области A_j1(G) величина y_j Î Y наиболее точно можно измерить в единицах Δ_{j 1}.

Вообще

│Δ_{j 0} - Δ_{j 1}│≥ 0

Обозначим

(30)

Пусть

τ_j^* = τ(P, N_j0 + N_j1 – 2) (31)

- критическое значение критерия Стьюдента при заданной доверительной вероятности P и степени свободы N_j0 + N_j1 – 2.

Для сопоставления между собой величин

Μ_{j 1} и Μ_{j 0}; j = j₀; j₀ = 1..N ,

оперируют следующими противоположными неравенствами [1]:

ç M_j1 - M_j0 ç < d _j^*τ_j^* (32)

и

ç M_j1 - M_j0 ç ≥ d _j^*τ_j^*, (33)

где

d _j^*τ_j^* > 0 (34)

При этом, если имеет место (32), то вероятностью P утверждают, что справедлива гипотеза:

y_j = M_j1 = M_j0.

А это означает что, в открытой области

A_j^* = (Μ_{j 0} - Δ_j ^* , Μ_{j 0} + Δ_j ^*)

при заданной вероятности P = P₀ все значения величины y_j Î Y являются практически друг от друга неразличимыми, где

Δ_j ^* = d _j^*τ_j^* (35)

В месте с тем, в закрытой области

A_j^* = [Μ_{j 0} - Δ_j ^* , Μ_{j 0} + Δ_j ^* ]

при заданной вероятности P = P₀ друг от друга различают следующие три значения величины

y_j Î Y:

y_j = Μ_{j 0} - Δ_j ^*, y_j = Μ_{j 0} и y_j = Μ_{j 0} + Δ_j ^*

В итоге, в области A_jk(G) ( k = 0,1) величина y_j Î Y фактически измеряется в единицах Δ_jk , а в области A_j^* в единицах Δ_j ^*.

Обозначим

Δ_jmax = max{ Δ_j0, Δ_j1, Δ_j ^*} (36)

Если бы запись (36) была бы корректной, то величину y_j Î Y можно было измерить в единицах Δ_jmax. И тогда в области

A_j0(G)ЩA_j1(G)ЩA_j^*

все значения величины y_j Î Y, как измеренные в одних и тех же единицах, были бы между собой сопоставимыми.

В действительности, однако, запись (36) не является корректной.

В самом деле, величины Δ_j0 и Δ_j1, согласно (6), (27) и (29) определяются с одним и тем же способом. Благодаря этому имеет место

Δ_j1 = Δ_j0 при S_j1 = S_j0 и N_j1 = N_j0

и, следовательно, вообще

│Δ_j1 - Δ_j0 │≥ 0

Что касается величине Δ_j ^*, то способ ее определения, согласно (30), (31) и (35), отличается от способа определения величин Δ_j1 и Δ_j0. По этой причине имеет место

Δ_jk ¹ Δ_j ^* при S_j1 = S_j0 и N_j1 = N_j0; k = 0,1

В итоге, запись

│Δ_jk - Δ_j^* │≥ 0

не является корректной. Следовательно, не является корректной и запись (36).

Обозначим

d K_j = S_jK и tK_j = t(P, 2(N_jK -1)) ; K = 0,1 (37)

Можно проверить, что

d 1_j t1_j = d 0_j t0_j = d _j^*τ_j^* при d _j1 t_j1 = d _j0 t_j0 > 0

d 1_j t_j < d _j^*τ_j^* при 0 < d _j1 t_j1 < d _j0 t_j0 (38)

d 0_j t0_j < d _j^*τ_j^* при d _j1 t_j1 > d _j1 t_j1 > 0

Как видно, величины

Δk_j и Δ _j^* ; k = 0,1

являются между собой сопоставимыми,

где

Δk_j = d k_j tk_j

Обозначим

d _j = d 1_j и t_j = t1_j при d 1_j t1_j £ d _j^*τ_j^*

и (39)

d _j = d _j^* и τ_j = τ_j^* при d 1_j t1_j > d _j^*τ_j^*

Согласно (38) и (39) имеет место

0 < d _j τ_j ≤ d 0_j t0_j ≤ d _j^*τ_j^* (40)

и, следовательно,

A_j(G) Í A_j(0,G) Í A_j^*(G), (41)

где

A_j(G) = [Μ_{j 0}(G) - d _j τ_j , Μ_{j 0}(G) + d _j τ_j ]

A_j(0,G) = [Μ_{j 0}(G) - d 0_j t0_j , Μ_{j 0}(G) + d 0_j t0_j ]

A_j^*(G) = [Μ_{j 0}(G) - d _j^*τ_j^* , Μ_{j 0}(G) + d _j^*τ_j^* ]

О множестве A_j(G) говорят, что оно является областью индивидуальной нормы величины

y_j Î Y для организма данного человека и пишут:

M_j(Z,G)Î A_j(G) (42)

Как видно, область индивидуальной нормы является подобластью как области с корректированной статистической нормой A_j(0,G), так и области A_j^*(G).

В итоге, согласно (41) и (42), имеет место

M_j(Z,G)Î A_j(G) Í A_j(0,G) Í A_j^*(G), (43)

т.е. точечная индивидуальная норма является общей точкой всех областей: A_j(G), A_j(0,G) и A_j^*(G).

Согласно (40) имеет место

ç M_j1 - M_j0 ç < d _j τ_j Þ ç M_j1 - M_j0 ç < d _j^*τ_j^* , (44)

Если

ç M_j1 - M_j0 ç < d _j τ_j; j = j₀; j₀ =1..N, (45)

то, согласно (44),

ç M_j1 - M_j0 ç < d _j^*τ_j^*; j = j₀; j₀ =1..N (46)

и, следовательно, с вероятностью P можно утверждать, что: M_j1 = M_j0.

Говорят, что функциональная часть организма человека, характеризуемая величиной y_j Î Y, находится в нормальном состоянии в широком смысле, если выполняется условие (45). А если выполняется условие (46), то говорят, что она находится в нормальном состоянии в обычном смысле.

Обозначим

a _j = (47)

Величины

a _j; j =1..N,

как видно, являются безразмерными и, следовательно, между собой сопоставимыми.

Обозначим

a = max{a _j, j =1..N} (48)

и

Δ_j = a MZ_j (49)

Согласно (47), (48) и (49) имеет место

Δ_j ≥ d _j t_j ; j = 1..N

Следовательно

ç M_i1 – M_j0 ç ≥ Δ_i Þ ç M_j1 - M_j0 ç ≥ d _j t_j для всех j = 1..N (50)

В том случае, когда существует хоть одно i = i₀ такое, что

ç M_i1 – M_j0 ç ≥ Δ_i; i = i₀; i₀ = 1..N, (51)

согласно (50), будет иметь место

ç M_j1 - M_j0 ç ≥ d _j t_j для всех j = 1..N (52)

и, следовательно, не выполнится ни одно условие

ç M_j1 - M_j0 ç < d _j t_j ; j = j₀ ; j₀ = 1..N

Таким образом, выполнение условия (51) достаточно, для того чтобы ни одна функциональная часть организма человека не находила в нормальном состоянии в широком смысле.

Каждая совокупность величин

M_j1, M_j0 , d _j и t_j ; j = j₀ ; j₀ = 1..N

служит характеристикой состояния вполне определенной, а именно j –ой функциональной части организма. Вместе с тем, выполнение условия (51), как только что было показано, приводит к тому, что ни одна функциональная часть организма человека не будет находиться в нормальном состоянии. Это можно объяснить, положив, что каждая величина Δ_j содержит в себе сведения о состоянии всех функциональных частей организма, т.е она является характеристикой всего организма.

При этом, согласно (37), (39), (47), (48) и (49), имеет место

Δ_j = Δ_j (P) > 0

Следовательно, выполняется условие

P ≤ P_max < 1,

где

P_max – максимально возможное значение величины P для организма данного человека.

Определение

Пусть, Δ_j(O,G) – значение Δ_j такое, что

Δ_j = Δ_j(O,G) при P = P_max

Тогда и только тогда говорят, что величина Δ_j(O,G) является объективной системной единицей измерения величины y_j Î Y в организме данного человека.

О величине Δ_j говорят, что она является оценкой Δ_j(O,G) и пишут [3, 4]:

Δ_j = Δ_j(O); j = 1..N (53)

Для величины Δ_j(O), согласно (49) и (53), имеет место

Δ_j(О) = Δ_j(О,P)

Следовательно, величина Δ_j(O), так и величина P, является субъективной характеристикой организма человека. О ней можно говорить, что она является субъективной системной единицей измерения величины y_j Î Y в организме данного человека.

Установление величин

Δ_j(О); j = 1..N (54)

и, в конечном счете, величин

M_j(О); j = 1..N, (55)

является важнейшим условием для объективного измерения состояния здоровья человека,

где

M_j(О) = round(,1) Δ_j(О) (56)

Польный алгоритм определения этих величин приведен [5]. Этот алгоритм справедлив как в том случае, когда решение принимается по единичным результатам обследования больного, так и в том случае, когда решается задача прогнозирования.

Литература

1. Ивлева Е.И. Повышение эффективности терапии больных невротическими

расстройствами на основе коррекции вегетативного гомеостаза. Автореф. дис.на соискание ученой степени КМН: 14.00.05 и 14.00.18 – Воронеж. 2001. - 23 с.

2. Большев Л.Н., Смирнов Н,В. Таблицы математической статистики. М.- Наука. Главная редакция физико-математической литературы. – 1983. – 416 с.

3. Естественный глобальный оптимум и вероятностный предел познания истины. Индивидуальная норма человека. http://www.medlinks.ru/article.php?sid=33435 

4. Вероятностный предел познания истины и вопросы математического моделирования живого организма как единого целого. http://www.medlinks.ru/article.php?sid=32701

5. Хускивадзе А.А., Хускивадзе А.П. Способ определения степени переносимости организмом больного с пневмонией активной ортостатической пробы. RU 2008140229 A . Бюл. № 6, 2009